Otra animación 3D matemática: Nature by Numbers

Este corto de animación realizado por Cristobal Vila expone elegantemente la intrincada relación que existe entre la naturaleza y las matemáticas a través de la conocida sucesión de Fibonacci descrita por Leonardo de Pisa. Además de la increíble calidad del trabajo de Cristobal Vila me gustaría destacar la música que aparece en el vídeo. El tema música se llama Often a Bird de Wim Mertens.

A continuación, voy a dar una pequeña base teórica que permitirá entender mejor los fundamentos matemáticos en los que se basa la animación anterior.
La animación arranca presentando una sucesión de números. Una serie muy famosa y reconocida desde hace muchos siglos en el mundo occidental gracias a Leonardo de Pisa, una matemático italiano del siglo XIII, también llamado Fibonacci. Por eso se la conoce como Sucesión de Fibonacci, aunque ya había sido descrita con mucha anterioridad por los matemáticos hindúes.

Se trata de una sucesión infinita de números naturales donde el primer valor es 0, el siguiente es 1 y, a partir de ahí, cada cantidad se obtiene sumando las dos anteriores.
Los valores de esta sucesión aparecen en numerosas aplicaciones, pero una de la más reconocida es la Espiral de Fibonacci, que siempre se ha utilizado como una aproximación a la Espiral Áurea (un tipo de espiral logarítmica) porque es más fácil de representar simplemente con la ayuda de un compás.
Eso es lo siguiente que se muestra en la animación, justo después de aparecer los primeros números de la sucesión: el proceso de construcción de una de estas espirales.

 Primero se van creando cuadraditos que corresponden a cada valor de la sucesión: 1x1 - 1x1 - 2x2 3x3 - 5x5 - 8x8, etc y se disponen de la manera que vemos en el gráfico de la izquierda.
A continuación podemos trazar un cuarto de arco de circunferencia (90º) dentro de cada cuadradito y fácilmente vemos cómo surge la Espiral de Fibonacci, a la derecha.
En la animación se ha introducido una pequeña corrección óptica para hacer que la curva resultante sea más parecida a una verdadera Espiral Áurea (más armoniosa y equilibrada), tal como se explica en la figura que aparece a continuación:

NOTA IMPORTANTE: aunque viendo la animación se transmite la idea de que la Espiral de Fibonacci (o la Espiral Áurea, tanto da) está en la base de la forma de un Nautilus, realmente no es así. Es curioso, porque si buscáis en Google Images: “espiral+nautilus” veréis cantidad de imágenes que sugieren que esta concha realmente se basa en el sistema constructivo descrito más arriba.

 Por tanto en la animación Cristoval Vila ha hecho trampa. O se podría explicar de un modo más “fino”, diciendo que se ha tomado una licencia artística.
Una vez que ha aparecido el Nautilus se da paso a la segunda parte de la animación. En ella se introduce el concepto de Proporción Áurea mediante la construcción de un Rectángulo Áureo. Para ello partimos de un simple cuadrado y utilizamos un procedimiento clásico que sólo requiere regla y compás. Lo podemos ver en la siguiente serie de ilustraciones:
Se trata un rectángulo muy especial y conocido desde antiguo. En él se cumple esta proporción, también conocida como Razón Áurea o Divina Proporción: el lado mayor (a) es al lado menor (b) lo que la suma de ambos (a+b) es al mayor (a).

El resultado de esta proporción (es decir, de la división de a por b) es un número irracional también conocido como Phi —no confundir con Pi— y con un valor aproximado de 1,61803399…
Antiguamente no se concebía como una verdadera “unidad” sino como una sencilla relación de proporcionalidad entre dos segmentos. Y podemos encontrarla en numerosas figuras creadas por el ser humano en el arte y la arquitectura, desde las civilizaciones Babilónicas o Asirias hasta nuestros días, pasando por la Antigua Grecia o el Renacimiento.

UNA CURIOSIDAD: no está evidenciada en la animación, pero existe una profunda relación entre la Sucesión de Fibonacci y la Proporción Áurea.

A la izquierda tenemos un ejemplo (luego veremos otro más): si vamos dividiendo cada valor de la Serie de Fibonacci por el anterior, el resultado tiende a Phi. Cuanto más altos son los valores, mayor es la aproximación (considerad que Phi, como todo número irracional, tiene infinitos decimales.

En la animación vamos un pasito más allá y llegamos a un nuevo concepto, quizás no tan conocido, pero igualmente importante: el Ángulo Áureo. Es decir, la relación angular de proporción entre dos segmentos circulares:

 Con estos dos segmentos circulares se sigue cumpliendo la misma proporcionalidad áurea, pero en este caso el valor del ángulo formado por el menor de ellos es otro número irracional, que podemos simplificar y redondear como 137,5º .
Y resulta que ese valor está muy presente en la naturaleza. Esto es lo siguiente que vemos en la animación: cómo se configura la estructura que forman las pipas de un girasol.
Fijáos en al siguientes figuras:

— Aportamos una primera pipa de color rojo.
— Giramos 137,5º
— Añadimos una segunda pipa de color verde y hacemos que la anterior se vaya hacia el centro.
— Giramos otros 137,5º
— Añadimos una tercera pipa de color tostado y hacemos que la anterior se vaya hacia el centro, hasta tocar con la primera.
— Giramos otros 137,5º…
… y así sucesivamente, pipa tras pipa, iríamos obteniendo paulatinamente unas distribuciones como las que tenéis en las siguientes figuras.

De este modo llegamos a la estructura característica en la que están dispuestas todas las pipas en su girasol, que es la más compacta posible. Siempre se ha dicho: la naturaleza es sabia :-)
OTRA CURIOSIDAD: ¿Recordáis que habíamos comentado que había una profunda relación entre la Sucesión de Fibonacci y la Proporción Áurea? Pues bien, a continuación tenemos otro punto de encuentro entre ambos conceptos. Fijaos en las siguientes imágenes de un girasol.

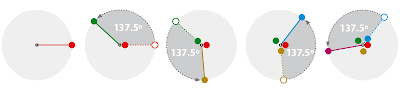
Si observáis atentamente la configuración de las pipas veréis cómo aparecen una serie de patrones en espiral. En la ilustración de la izquierda tenéis resaltadas tres de las tipologías de espirales que podemos encontrar.
Pues bien: si os centráis en una de las tipologías, por ejemplo la que aparece en verde, y os vais a la ilustración superior derecha podréis comprobar que se cuentan un número determinado de espirales como ésta, concretamente 55 espirales. Casualmente un número que está dentro de la Sucesión de Fibonacci.

 

Y en las dos ilustraciones de la derecha tenéis los otros casos, en azul y naranja, que nos proporcionan unos valores que también se hallan dentro de la sucesión: 34 y 21 espirales.
En principio, todos los girasoles del mundo muestran una cantidad de espirales que se hallan dentro de la Sucesión de Fibonacci. Podéis comprobarlo saliendo al campo y buscando una plantación.
También podéis usar la imagen de un girasol real o acudir a http://www.maths.surrey.ac.uk donde aparece explicado, junto a otras curiosidades.
A propósito: os recomiendo el resto de la página de Ron Knott (http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/), un matemático de la Universidad de Surrey, en Inglaterra: está llena de información muy valiosa y didáctica, todo muy bien explicado y con grandes dosis de elementos curiosos.

Para terminar llegamos a la tercera parte de la animación en la que se trabaja con un concepto un poco menos conocido que los anteriores: las Teselaciones de Voronoi, también conocidas como Polígonos de Thiessen.
Comentaros que este tema lo descubrí gracias a la página de Héctor García (www.kirainet.com), que visito prácticamente a diario (y que a pesar de ser un blog dedicado a la cultura japonesa y todo lo que tiene que ver con aquel país, de vez en cuando también nos regala con otros temas interesantes, como éste de Delaunay y Voronoi).
Estas formaciones geométricas se basan en un patrón de distribución que resulta fácilmente reconocible en muchas estructuras naturales, como las alas de los insectos o las ramificaciones capilares vegetales.
También es ampliamente utilizado para optimizar los sistemas de distribución basados en áreas de influencia, a la hora de decidir, por ejemplo, dónde se instalan las antenas de telefonía o las diferentes delegaciones de una cadena de pizzerías.
Veamos un sistema muy intuitivo de entender cómo se conforma una Teselación de Voronoi:

Imaginad que tenemos dos puntos: uno rojo y otro azul (arriba a la izquierda). Empezamos trazando una línea que los une y después otra perpendicular que se halle justo en la mitad. Acabamos de hallar la mediatriz del segmento de unión de estos dos puntos.

Arriba a la derecha añadimos un tercer punto verde y generamos dos nuevas mediatrices, que se interseccionan con la primera.
Si seguimos añadiendo puntos podremos ir generando sucesivas mediatrices que, con sus intersecciones, darán lugar a una serie de polígonos —Teselas de Voronoi— alrededor de un conjunto de “puntos de control”. De esta manera, el perímetro de los polígonos generados es equidistante a los puntos vecinos y designa su área de influencia.

Los segmentos que unen directamente los puntos forman una estructura triangular conocida como Triangulación de Delaunay. En la siguiente ilustración podéis ver el proceso conforme vamos añadiendo puntos: También encontraréis sistemas interactivos en la red, como el de la página web http://www.pi6.fernuni-hagen.de/GeomLab/VoroGlide/index.html.en, para ir añadiendo puntos, moverlos y comprobar cómo se actualiza la estructura.

En realidad, si tenemos una serie de puntos aleatorios dispersos en el plano, la mejor forma de hallar la Telesación de Voronoi correspondiente a ese conjunto es partir de la Triangulación de Delaunay. Y de hecho ese es precisamente el orden que se muestra en la animación: primero aparece la Triangulación de Delaunay y posteriormente la Teselación de Voronoi.
Pero para poder trazar una correcta Triangulación de Delaunay es necesario que se cumpla la conocida como “Condición de Delaunay”: una red de triángulos es una triangulación de Delaunay si todas las circunferencias circunscritas de todos los triángulos de la red son “vacías”.
Fijaos que realmente, dados un número determinado de puntos en el plano no existe una única manera de unirlos formando triángulos, existen muchísimas. Pero sólo una posible triangulación cumple con la mencionada condición. Es muy simple: trazaremos un triángulo usando 3 puntos sólo si se cumple que la circunferencia circunscrita a esos 3 puntos es “vacía” (no encierra ningún otro punto).

También encontraréis sistemas interactivos en la red, como éste, para ir añadiendo puntos, moverlos y comprobar cómo se actualiza la estructura.

En realidad, si tenemos una serie de puntos aleatorios dispersos en el plano, la mejor forma de hallar la Telesación de Voronoi correspondiente a ese conjunto es partir de la Triangulación de Delaunay. Y de hecho ese es precisamente el orden que se muestra en la animación: primero aparece la Triangulación de Delaunay y posteriormente la Teselación de Voronoi.
Pero para poder trazar una correcta Triangulación de Delaunay es necesario que se cumpla la conocida como “Condición de Delaunay”: una red de triángulos es una triangulación de Delaunay si todas las circunferencias circunscritas de todos los triángulos de la red son “vacías”.
Fijaos que realmente, dados un número determinado de puntos en el plano no existe una única manera de unirlos formando triángulos, existen muchísimas. Pero sólo una posible triangulación cumple con la mencionada condición. Es muy simple: trazaremos un triángulo usando 3 puntos sólo si se cumple que la circunferencia circunscrita a esos 3 puntos es “vacía” (no encierra ningún otro punto).
Podéis verlo en la siguiente gráfica, extraída de la Wikipedia:

Una vez que tenemos definida la Triangulación de Delaunay (izquierda) podemos ir girando 90º cada uno de los segmentos de los triángulos por el punto medio para dar con la Teselación de Voronoi (derecha). Exactamente lo que muestra la animación justo antes de alejarnos y mostrar la estructura del ala de nuestra libélula.

También podríamos utilizar los centros de cada circunferencia, marcados en rojo, ya que describen los vértices de las Teselas de Voronoi.

Por supuesto, estoy seguro de que si tomaramos una libélula real y analizasemos sus alas con la ayuda de una lupa o un microscopio, encontraríamos excepciones y desviaciones. Pero es indudable la similitud de ambas estructuras. 

Publicado por Pedro
Ilustraciones de Cristoval Vila 

Este obra está bajo una Licencia Creative Commons Atribución-NoComercial-SinDerivadas 3.0 Unported.